Lattice Embeddable Graphs- Some general ideas
It's time to summarize our findings on lattice embeddable graphs! Today, we'll wrap up our ideas about this topic with some general thoughts for the future. There are many open questions, and as such I may be posting about this in future when more is discovered. I highly encourage you to give this a go, and share your thoughts with me in the comments and by email!
Criteria for an embedding
We've already seen some criteria for an embedding. Notably, we've seen that if a graph is non-planar, non-connected (technically, see later), or has a higher connectivity than that of the lattice, it won't embed. What else can we say?
Examples of our current non-embedding criteria.
Let's take, for the sake of example for this post and without loss of generality, the lattice L3H. We've seen this lattice many times, primarily due to its simplicity. Will the graph below embed on L3H?
The graph 3L(1). Will it embed on L3H?
It won't embed! Why? It should, based on our criteria above. We've missed something.
Forbidden Cycles
There are certain features of graphs, called cycles. These are a loop of vertices that close up on each other, like in our graph 3L(1).
The reason that 3L(1) does not embed on L3H () is due to the 3-cycle present in the graph. There is nowhere in L3H that a 3-cycle can embed! As such 3L(1) cannot embed on L3H (and, in fact, ANY 3L(...) graph can't embed on L3H).
What can we say now, given this insight?
For every lattice, there are only certain sizes of cycles that can embed on it. For instance, on L3H, no graph with a 3-cycle, 4-cycle, or 5-cycle can embed. Hopefully this is obvious by looking at the lattice cell!
However, 6-cycles ARE allowed, and need to be considered when looking at the graph generalisation procedure from "A Multidimensional Complexity Onion". It's very easy to miss a potential opportunity to create a loop, so if you've missed these before, fear not! I've fallen fowl of this several times :P
So, let's have another look at a graph and see if it embeds on L3H. Can you figure it out before I tell you?
The graph 6L(1{4³}). Does this embed on L3H?
Just looking at the three criteria above:
- The graph is planar and connected
- The graph has maximum connectivity 3
- The graph has no 3, 4, or 5-cycles
Naïvely, given it fits these three criteria, we'd expect it to embed. However, spoiler alert: it doesn't. Why is this?
The problem is the bridge.
To explain why this is the problem, we're going to have to bring in a new concept: Bridging Numbers.
Bridging Numbers of a Graph
The Bridging Numbers Bⁿₘ() of a Graph G(V,E) are defined as the largest number of paths of length m between two nodes separated by n nodes. When n=1, these are sometimes written Bₘ(G(V,E)). As an example using G = 6L(1{4³}), the maximum number of paths of length 2 between any two vertices separated by 2 vertices is 3, so B²₂(G) = 3. These vertices are the two vertices of connectivity 3.
Bridging Numbers of a Lattice
Bridging Numbers are also defined on a Lattice L. The definition is as above, replacing G with L. Of course, as L is infinite, these are much harder to compute- a Lattice has an uncountably infinite number of bridging numbers, whereas a graph has finitely many! There is also one other complication: Not all vertices in a lattice are equivalent. As such we need to calculate several sets of lattice numbers and choose the highest number we find for any chosen n,m. I have calculated the B¹ₘ bridging numbers for several lattices, and these are given below. I will elaborate on the method I used in a small follow-up blog post for those that are interested.
The Bridging Numbers B¹ₘ(L) for several lattices, calculated by computer code.
Now we know what Bridging numbers are, what can we say about thier role in lattice embeddings?
Pulling It All Together
As far as I can tell, these four criteria are both necessary and sufficient to characterise all lattice graphs for any Lattice we've discussed so far:
- The Graph must be Planar
- Every vertex of the Graph must be of equal or lower connectivity than the lattice connectivity
- The graph must not contain any forbidden cycles, characterised by the lattice
- The graph must have all bridging numbers Bⁿₘ(G) equal or lower to the equivalent bridging numbers Bⁿₘ(L) of the lattice.
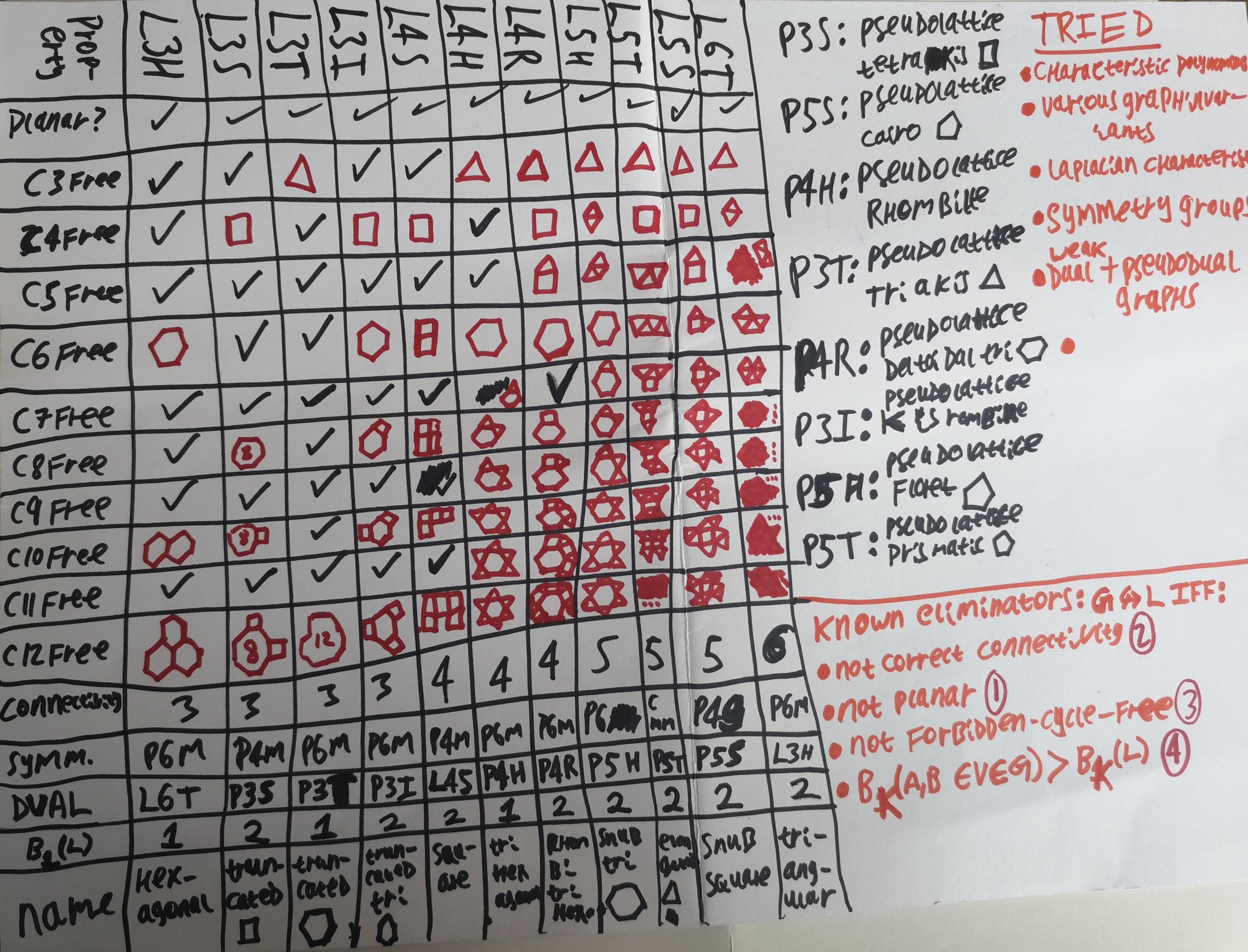
A table of all the information we've discussed (and some we haven't), for various lattices, as well as some wrong avenues I took before arriving at these 4 conditions. Sorry about the quality of the photo. This was the best I could do.
I have not been able to find a graph and lattice that satisfy these conditions yet does not embed. I have not been able to prove these statements, particularly the last statement, but I have not found a counterexample and I believe these to be the only 4 conditions we require. I also suspect the third is redundant but I have not been able to prove this either. A more experienced graph theorist is welcome to come along and disprove or prove any of these!
Next, here are the numbers of lattice graphs on a few of the simpler to draw lattices:
Some lattices and their respective numbers of lattice graphs of vertex number n.
Finally, let me present some generalisations of these ideas we've talked about.
Taking it Further
Now we've talked about our main theorem and presented the work we've done so far to solve it, let me now talk about how we can take it further.
Our first idea to discuss is the concept of Connected Graphs. Put simply, a connected graph is one which only has a single piece. If you picked up the graph by one of its vertices, and gave it a shake, nothing would come apart (that analogy isn't strictly true- most notably it breaks down when we talk about topological graphs, but it's fine for now). Another, better definition is that there is a path of vertices and edges from every vertex to every other vertex.
Every graph we've looked at has been a connected graph, and I've restricted our discussion to them on purpose. However our theorem never mentions the connectedness (not to be confused with the connectivity!) of the graph, and we can think of graphs that are disconnected that will embed on our lattices!
No work has been done on disconnected graph embeddings at this time. I leave it to you to investigate for now!
Another generalisation is lattices of differing connectivity. So far we've only looked at semiregular lattices, which have a constant connectivity. However, we can think of many, many more lattices that satisfy some, but not all, of our lattice properties. I'll draw 3 of each of them below:
3 aperiodic, planar lattices of constant connectivity, and 3 periodic, planar lattices of differing connectivity.
Finally, we can even relax the Planarity condition for both lattices and graphs!
A lattice without the Planarity condition.
Little work has been done on these cases at present.
What is all this good for?!?
We'll round out this post by saying what all this could be used for. I'm aware this post is rather long and rambling, so I'll keep it short: does it need an application? We've had fun, haven't we? Isn't that enough?
Ok, ok, that attitude doesn't get research funding.
Here's 5 applications off the top of my head:
- Chemistry: Graph Theory is used to predict certain properties of molecules, particularly their conductivity and such. This could potentially be used in much the same way.
- Nanomaterials Science: knowing what chemicals fit on certain infinite lattices of chemicals (L3H remind anyone else of graphene?) could possibly be useful in designing new composite nanomaterials.
- Theoretical Physics: There's something called Loop Quantum Gravity. I don't know much about it to say anything with any form of confidence but I do know that uses graph theory and something called a "spin lattice" so...
- Integrated Circuits: This is probably the closest to an actual application as this has. Represent a surface as a 2d lattice. The lattice graphs that embed on it are the possible layouts of the circuits on the surface.
- Social Networking Theory: Again, an actually useful application. Presenting a social network as a graph is common. Making it look pretty is pretty hard. Lattice embeddings should make it easier.
Hopefully that satisfies your curiosity!
Now then, I think it's time for something completely different. We've talked about graph theory extensively, and I think we need a rest! I think it's fair if we relax with a game of dice...
-Wolfie <3