Brute Force and Hexes
In our last post, we learned what a lattice is, and before that, we learned what a graph is. It's time to combine the two.
Before we begin, it's time for some shorthand notations, as drawing an infinite lattice is hard.
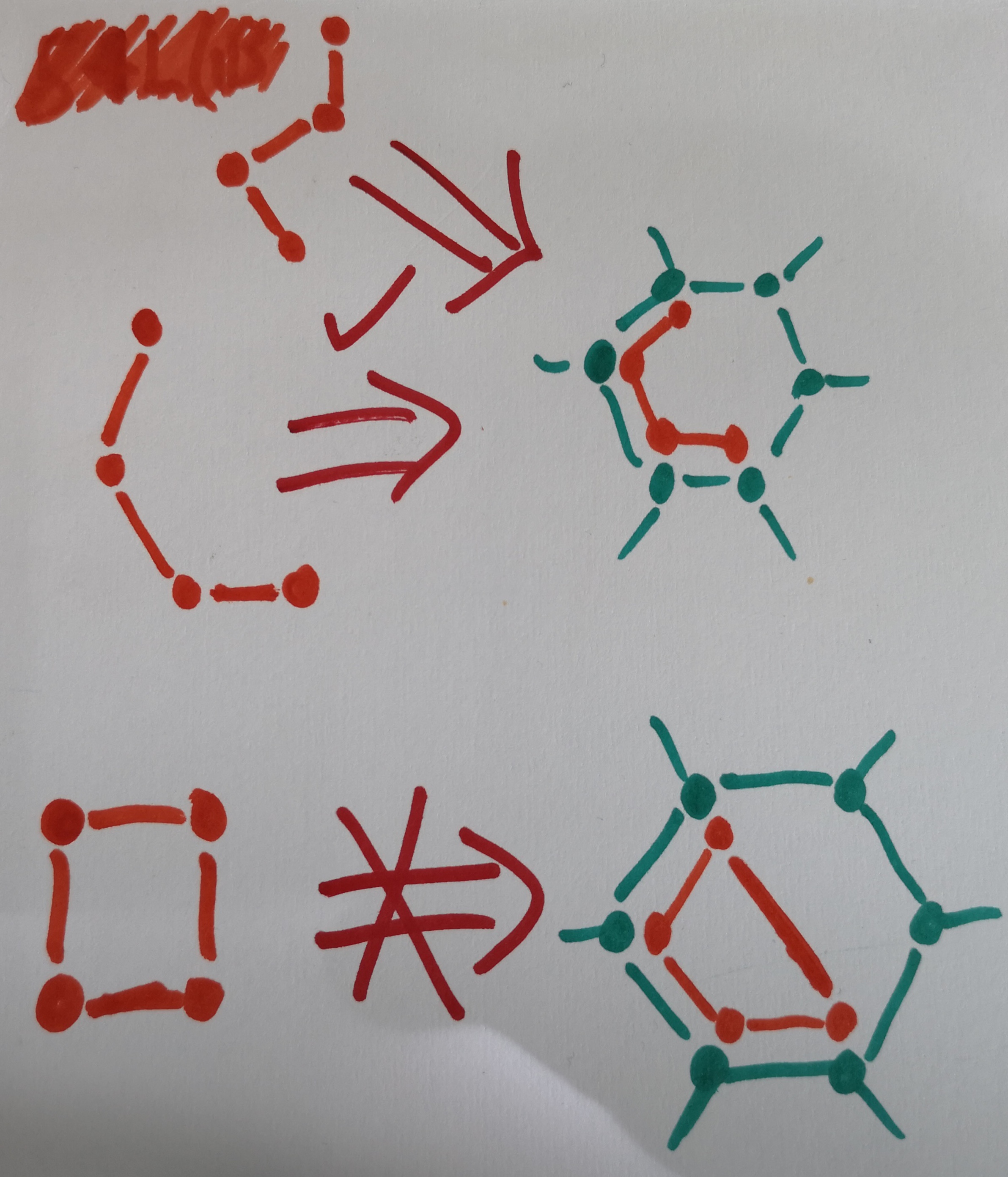
A graph in orange. A lattice cell in green. A question arrow in black. Don't worry about the written shorthand for now.
We can draw our graphs as normal, but we'll introduce a graph shorthand in the next post. However, we'll now only draw the repeating part of our lattice- called the lattice cell- with edges going off to imaginary vertexes to indicate its tiling property.
Now, let's state the main theorem we are trying to solve.
The main theorem
Here is the full theorem in all its glory:
Given a lattice L of constant connectivity N and class X, which planar graphs G(V, E) can be embedded on L?
That's... Intimidating, isn't it? Don't worry, we'll unpack it piece by piece.
Given a lattice L...
We know what a lattice is. "Given" just says that we need to choose a lattice in order to solve the problem.
...of constant connectivity N and class X...
These are just our parameters for our lattice- because they may be useful to know when trying to prove anything. Our "constant connectivity N" is as it was in the last post- the number of edges from each vertex in the lattice, e.g 3. "Class X" is simply our way of distinguishing between lattices of the same connectivity- Hexagonal, for instance.
...which planar graphs G(V, E)...
In our first post, we discussed planar graphs. They're the graphs that can be drawn without edge crossings on a 2D plane. G(V, E) is simply the way mathematicians write a generic graph. The (V, E) is simply to show that the vertexes and edges are objects that behave differently to each other.
...can be embedded on L?
Three examples of attempted embeddings. Only the top two graphs embed on this lattice (L3H).
This is the tricky part. To embed something, in the mathematical sense, means that some structure is contained within another structure (formally, there is an injective map from the embedded object to the space it's embedded in). To put it into completely concrete terms for our problem, if you draw a graph on top of your lattice, and all of the edges and vertices of the graph line up with a subset (as each is infinite) of the vertices and edges of the lattice , you have a successful embedding. If you try every single possibility of drawing your graph on the lattice and none of them work, you don't have an embedding, and so that graph isn't embeddable on that lattice. It might be on another lattice however!
A concrete, worked example
Now we can explain the title of this post. We're going to look at L3H, the infinite Hexagonal lattice of connectivity 3, and see which graphs can be embedded on it.
First, let's draw our lattice. I'll draw it with vertexes hollow, so I can colour them in to show the embeddings.
Next, we'll start with a single vertex. Can a single vertex be embedded on L3H?
Is this an embedding?
Yes, yes it can. Let's stick on an edge and another vertex.
How about now?
Again, we have an embedding! Let's make a table of our results:
A table of our results so far.
What about for 3 vertices? We have 2 planar graphs. Let's check them both:
Checking both 3-vertex graphs...
It turns out that only one of the 3-vertex planar graphs is embeddable onto L3H!
Those of you who are paying attention might be able to spot what we're about to do, but honestly this next step took me a few weeks to actually work out. Instead of checking all planar graphs, which would take forever, we can instead use our knowledge that we've already gained to simply the problem massively.
However, we'll need to say a few things about our graphs first... And that will have to wait until next time, I'm afraid. This post is getting long in the tooth. But I promise that next time we'll really make some headway with this project!
-Wolfie <3